
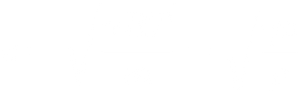
c = speed of sound (ms⁻¹)
E = Bulk modulus (Pa)
ρ = Density (kg m⁻³)
Speed of sound in a solid:
Speed of sound in a gas:
c = speed of sound (ms⁻¹)
γ = Ratio of specific heats
R = molar gas constant (J mol⁻¹ K⁻¹)
T = Temperature (K)
m = Molar mass of gas (kg mol⁻¹)
p = Pressure (Pa)
ρ = Density (kg m⁻³)
For this equation, notice that, if Boyle's Law is obeyed, p/ρ is constant, so the speed of sound will be independent of a change in pressure.
Speed of sound in a stretched string or wire:

c = speed of sound (ms⁻¹)
T = Tension (N)
μ = Mass per unit length (kg m⁻¹)
EQUATIONS TO CALCULATE THE SPEED OF SOUND IN VARIOUS SITUATIONS
The bulk (compressive) modulus will give you the speed of longitudinal waves in the substance. If you use shear modulus instead, it will give you the speed of transverse waves in the body of the same substance. In practice, this is used in calculations involving seismic waves
You can use this equation to explain why your voice goes high-pitched when you breathe Helium gas (not that I'm recommending doing so without first doing a full risk assessment).
The density of Helium at stp is ≈ 0.164 gcm⁻³, compared to air at ≈ 1.2 gcm⁻³ (i.e. about 7 times less). Since the speed of sound in a gas is inversely proportional to the square root of the gas’s density, the speed of sound in Helium is therefore about 2.7 times faster than in air (about 970 ms⁻¹). Wavelengths are constant in the human voice, since the dimensions of the standing waves are determined by the physical dimensions of the throat/mouth/nasal cavity etc., so the frequencies of the voice shift up by almost three octaves when breathing Helium.
Speed of sound in a gas as a function of RMS particle speed:

c = speed of sound (ms⁻¹)
γ = Ratio of specific heats
vᵣₘₛ = root-mean-square speed of gas molecules
This just comes from the previous equation by substituting in p = 1/3 ρ <c²>, which you might derive in thermodynamics lessons. It's nice to show that the speed of sound is very simply related to the speed the molecules are typically travelling at - if the particles in a gas move faster (e.g. because of a rise in temperature), then it is probably logical that sound waves will be passed on quicker.