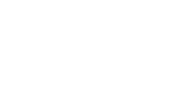ELECTROMAGNETIC FORMULAS
EQUATIONS TO FIND B FOR VARIOUS WIRE ARRANGEMENTS
-
All the equations below apply to wires and coils in a vacuum (or air, at a pinch).
-
Also in all cases, μ₀ = 4π x 10⁻⁷ Hm⁻¹ and I is the current in the wire or coil, in Amps.
B at perpendicular distance x from a straight wire:

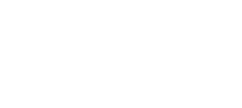
B at centre of a flat coil with N turns of radius r:
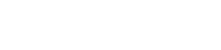
B at centre of an infinitely long solenoid with n turns per unit length:
In practice, this equation also applies quite well to the field well inside a finite-length solenoid if the solenoid is about 5 times longer than its radius or more, i.e. fairly long and thin. The shorter and fatter the solenoid gets, the closer it gets to acting like a flat coil.
The general formula for a solenoid of finite length is more complex, but the graph below shows you how closely it approaches the simpler formula when L ≳ 5r. Notice also, though, that B is only about half of this value at the ends of the solenoid.
B between a pair of Helmholz coils, each with N turns of radius r and separated by the same distance r:

Here's the Excel file used to plot the graph above - you can change the values of L and r to see what happens to the shape of the field: